nLab structural rule
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Structural rules
Idea

General
In formal logic and type theory, by the structural inference rules [Gentzen 1935 §1.2.1, 1969, §1.21] of a deductive system one means those inference rules which make no reference to logical operations but only to the unstructured premises of a deduction.
In standard intuitionistic logic (intuitionistic type theory) the structural rules notably include the weakening rule and the contraction rule in the antecedent, which exhibit context extensions as admitting natural diagonal and projection maps, respectively, hence as admitting interpretation as cartesian products (cf. Jacobs 1994):
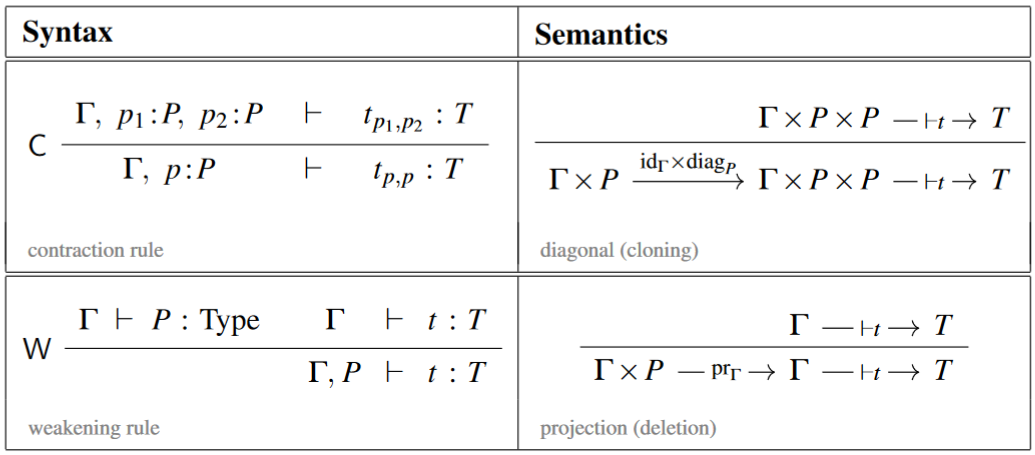
Discarding these rules leads to linear logic (linear type theory).
Generally, logical systems discarding some structural rules are called substructural logics.
In dependent type theory
In (intuitionistic) dependent type theory the structural rules include (e.g. Jacobs (1998), p. 122, UFP13, A.2.2, Rijke (2018), Sec. 1.4):
-
the variable rule,
-
the weakening rule,
shown in the following table together with their categorical semantics of dependent types:


Examples
Sub-structural logic
If some of the structural rules are not imposed in a formal logic one speaks of substructural logic.
For instance, if the weakening rule and contraction rule are omitted, one speaks of linear logic/linear type theory (see there), since then the logical conjunction is no longer consrained to behave like a Cartesian product but may behave like a non-cartesian tensor product.
References
The notion of the structural inference rules originates (under the German name Struktur-Schlußfiguren) with
-
Gerhard Gentzen, §1.2.1 in: Untersuchungen über das logische Schließen. I, Mathematische Zeitschrift 39 1 (1935) [doi:10.1007/BF01201353]
-
Gerhard Gentzen, §1.21 in: Investigations into Logical Deduction, in M. E. Szabo (ed.), The Collected Papers of Gerhard Gentzen, Studies in Logic and the Foundations of Mathematics 55, Springer (1969) 68-131 [ISBN:978-0-444-53419-4, pdf]
Review:
- Anne Sjerp Troelstra, §1.5 in: Lectures on Linear Logic, CSLI Lectures notes 29 (1992) [ISBN:0937073776]
Their categorical semantics is made explicit in:
- Bart Jacobs, Semantics of weakening and contraction, Annals of Pure and Applied Logic 69 1 (1994) 73-106 [doi:10.1016/0168-0072(94)90020-5]
Discussion in dependent type theory:
-
Bart Jacobs, p. 122, 585 in: Categorical Logic and Type Theory, Studies in Logic and the Foundations of Mathematics 141, Elsevier (1998) [ISBN:978-0-444-50170-7, pdf]
(emphasis on the categorical model of dependent types)
-
Univalent Foundations Project, §A of Homotopy Type Theory – Univalent Foundations of Mathematics (2013) [web, pdf]
(in the context of homotopy type theory)
-
Egbert Rijke, Dependent type theory [pdf], Lecture 1 in: Introduction to Homotopy Type Theory, lecture notes, CMU (2018) [pdf, pdf, webpage]
(in the context of homotopy type theory)
Last revised on September 4, 2023 at 09:56:46. See the history of this page for a list of all contributions to it.